本篇文章内容由[中国幕墙网ALwindoor.com]编辑部整理发布:
摘要:为了营造建筑复杂表皮,越来越多的建筑外表面使用曲面玻璃幕墙,玻璃冷弯作为曲面玻璃的重要成型手段之一,由于其无需特殊的玻璃加工工艺以及模具开模,可达到实现建筑形体的效果和降低玻璃造价的双重目标。然而,对于玻璃冷弯产生的玻璃应力的计算,往往采用有限元(词条“有限元”由行业大百科提供)模拟的方式,对于冷弯形态多样的异形建筑,全盘有限元验算将会花费巨大的计算开销,不利于设计初期的建筑迭代与几何优化。

为此,本文以弯曲板面应力公式推导为基础,对于单点翘曲与长边起拱两种常见冷弯模式,通过变形后的几何形态方程,推导出玻璃冷弯产生的弯曲应力,并借用建筑幕墙规范中对于大挠度弯曲薄板的折减系数表格,推导出考虑薄膜应力后的总应力的简化计算公式,并对公式进行有限元验证。
此外,对以上两种常见冷弯模式玻璃应力进行参数分析,得出玻璃冷弯应力主要与玻璃曲率变化量有关的结论,为任意形状玻璃冷弯应力简化计算打下基础。
关键词:玻璃冷弯,几何非线性,大挠度弯曲薄板

1 引言
曲面表皮的建筑由于其在美学上的价值和建筑表达上的自由,在近年来越来越受到建筑师和业主的青睐,也给作为运用最广泛的建筑外表皮材料之一的玻璃设计带来挑战。
对于曲面玻璃的生产工艺,一般来讲有冷弯和热弯两种方式:其中冷弯玻璃工艺是指,当玻璃成型之后通过机械方式对于玻璃边部或者角部施加外力,使玻璃产生变形,使得玻璃终态呈现出的形状与出厂时的形状有所区别的弯曲方法;热弯玻璃工艺则是指,在玻璃在工厂中的制作过程中玻璃原片在加热软化的状态下产生弯曲,冷却(词条“冷却”由行业大百科提供)后呈现弯曲的状态。
由于热弯玻璃的复杂工艺,往往需要专门的设备和加工能力,才能实现高质量的热弯玻璃。故热弯玻璃的极限板幅大小,严重受到热弯工艺和设备的影响,玻璃单价也根据弯曲的复杂程度和板面大小相比平板玻璃有所不同程度增长,同时,相比平板玻璃,热弯玻璃的生产周期也大大增加,玻璃的镀膜选择也因玻璃弯曲需要受热而受到限制。此外,由于近年来建筑形体设计更加的自由,甚至渐渐出现全楼板块均无平板玻璃的状况,全楼采用热弯玻璃甚至热弯多曲玻璃的方法,对工程的造价控制和工程工期均产生巨大的影响。因此,对于弯曲以及翘曲程度尚且有限的玻璃板块,采用生产与目标形态相近的平板玻璃或者单曲玻璃,随后在工厂或现场通过机械方式对于玻璃边框或角部施加外力,使得玻璃产生变形以近似建筑目标表皮形状,是更加适合于实际工程的弯曲玻璃的方法,其同时达到了实现建筑目标形体的效果和降低玻璃幕墙造价和工期的目标。
玻璃的冷弯是在玻璃加工完成后施加外力产生的,将会使得玻璃内产生额外的内力,且由于玻璃在其使用过程中将一直保持此冷弯力的作用以保持其弯曲造型,此内力需要与玻璃受到的其他荷载(如风荷载)等进行组合,校核玻璃的强度,以保证其安全性。
国内现行关于玻璃和幕墙的规范中,对于玻璃的冷弯计算均未有所提及,目前行业内的标准做法是采用有限元模拟计算软件中采用壳体单元建模,提取玻璃的原始形状(玻璃出厂形状)和目标形状(冷弯后形状),在玻璃的边部施加强制位移,计算出玻璃的内力,以作为玻璃强度校核依据。然而由于有限元计算开销较大,处理手段复杂等原因,此方法往往适用于少量典型板块的计算,即仅对最不利板块进行校核即可覆盖全楼最不利工况的情况。对于形状复杂的项目,往往单独依靠冷弯玻璃无法满足最不利工况,需要部分采用冷弯玻璃,部分采用热弯玻璃,方可实现。对于此类项目,往往需要对于全楼玻璃进行批量计算来确定平板与曲面玻璃分区的情况,由于每块玻璃的冷弯量和其他荷载(如风荷载、重力分量等)也处处各异,采用包络的算法无法满足项目设计的需求,而每块玻璃板面均采用有限元的计算的方法将耗费巨大的计算开销,面对此类项目,工程上往往采用规定最大冷弯量的方法来对玻璃进行分区,即对于建筑给定的曲面进行平面(词条“平面”由行业大百科提供)或圆柱拟合后,测量原曲面与拟合曲面的距离即为玻璃需冷弯量,将此量与给定的可容许冷弯量进行对比,来判断此板块是否可以通过冷弯来实现。然而,这种通过控制容许冷弯量的简化算法忽略了玻璃冷弯的具体形状、板块大小、其他荷载的组合等参数的影响,对于容许冷弯量的设定也往往根据保守的经验和有限的计算,往往无法得到令人满意的结果。
针对于此,本文将针对于玻璃冷弯的常见情况,进行玻璃冷弯计算的公式推导,旨在找到简化并精度尚可的手算公式,并对手算公式加以有限元验证,以便得出满足工程精度的简化冷弯玻璃应力手算方法,为冷弯玻璃快速批量计算打下基础。
2 单片玻璃冷弯应力计算
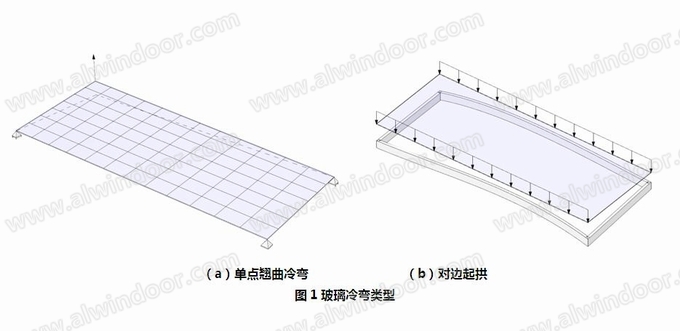
玻璃冷弯常见的模式往往可以被简化分解为以下两种(见图1):
(1) 单角翘曲
(2) 对边起拱
常见的玻璃冷弯变形可被分解为以上两种形式或其叠加,故将首先分别研究此两种冷弯模式下玻璃冷弯应力公式。
2.1 单角翘曲冷弯荷载下单片玻璃应力计算简化公式
对于平板玻璃,最常见的冷弯方式即为单角翘曲(见图1a),即在两条邻边固定(词条“固定”由行业大百科提供)的情况下,将此两条固定邻边夹角的对角角点向玻璃平面外施加强制位移,使玻璃此角点离开玻璃平面,形成玻璃四个角点不共面的马鞍形曲面。
根据板壳力学理论,薄板小挠度以弯曲为主,而薄板大挠度弯曲情况下,薄板的应变模式为弯曲作用与薄膜作用的结合。对于冷弯荷载下玻璃的应力计算也同样应该考虑玻璃由于弯曲产生的弯曲应力与玻璃表面由于拉伸(词条“拉伸”由行业大百科提供)产生的中面薄膜应力的叠加。
2.1.1 单角翘曲冷弯荷载下玻璃弯曲应力
角点翘曲产生的弯曲应力为玻璃冷弯应力的主要组成部分,其产生原因是由于平板玻璃角点翘曲,使得玻璃表面产生弯曲变形,进而形成弯矩以及上下表面的弯曲应力。对于翘曲量较小的情况,即大多数的冷弯工程案例中,此冷弯后曲面近似于一个双曲抛物面,而当冷弯量大于一定值时玻璃面产生屈曲失稳,导致其形状与双曲抛物面产生较大差距[2]。绝大多数工程中涉及到的玻璃冷弯量远小于玻璃面产生屈曲失稳的临界冷弯量,本文中仅研究工程中经常涉及到的冷弯荷载范围内的玻璃应力计算。
基于此假设,对于翘曲量较小的情况,我们可以根据双曲抛物面方程对玻璃变形后的主曲率进行推导。对于边长分别为 和 的矩形板面,当角部翘曲量为 时,其对应的双曲抛物面(见图2)方程为:
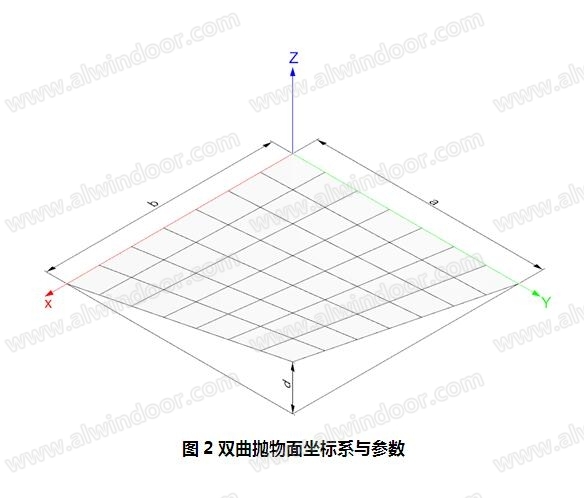


对于玻璃角点翘曲产生的弯曲作用导致的玻璃应力在玻璃上不同位置的分布,可以通过以上公式中带入全板面不同位置的 进行对比。取较典型的玻璃幕
墙板块(4500mmx1750mm),角部翘曲100mm,玻璃厚度10mm为例,代入板块中不同位置坐标,计算得到的应力分布如下:

由结果可见,玻璃角点翘曲产生的薄板变形,其中仅考虑弯曲作用导致的玻璃应力在整个板面上的分布比较均匀。从工程角度出发,可以忽略不同部位应力的差别,可用(0,0)点处计算得到的应力代表整个板面的最不利弯曲应力。
2.1.2 单角翘曲冷弯荷载下玻璃薄膜应力
由板壳力学理论可知,当板面挠度与板面厚度之比不大于1/5时,归结为小挠度问题,当超出此比值时,即为大挠度问题,即需考虑几何非线性的影响,其中面应力(薄膜应力)需要被考虑在内,以验证玻璃的强度。冷弯玻璃角点翘曲量往往会大于板面厚度的1/5,如忽略此薄膜应力往往造成玻璃内应力的低估,故此处需要对薄膜应力进行计算与考虑。
对于薄膜应力的计算,其理论推导公式较为复杂,在工程上应用较为不便。对于四边支撑的玻璃板,在建筑幕墙工程规范中,将玻璃的薄膜应力产生的效应与玻璃变形的关系用表格的方式表示出来(见表2),可通过查表的方式考虑薄膜效应对于玻璃板面应力和变形的有利作用[1]。对于玻璃冷弯产生的薄膜应力,可利用此表格,通过将冷弯变形状态近似等效为四边支撑玻璃板的变形状态,进而根据变形量相关参数查表反推薄膜应力产生的放大效应。
具体而言,根据《玻璃幕墙工程技术规范》中公式,四边支撑承受均布荷载使得玻璃产生大挠度弯曲导致的薄膜应力的折减系数可通过参数 进行查表得到[1]。为了在单点翘曲冷弯工况下使用此表格,需根据冷弯的变形量推导出等效的参数 。


 2.1.3 单角翘曲冷弯荷载下单片玻璃应力简化公式有限元验证
2.1.3 单角翘曲冷弯荷载下单片玻璃应力简化公式有限元验证
为了验证以上公式的准确性以及适用条件,对于典型的板面单角翘曲冷弯工况,利用Ansys软件建立有限元模型施加角部翘曲荷载,与以上玻璃应力公式计算的结果进行对比。对于典型板块的尺寸以及翘曲量见表4。

利用Ansys 18.1,采用SHELL181单元模拟玻璃面,玻璃基本尺寸取4500mmx 1750mm板块,玻璃厚度为10mm,玻璃采用
弹性材料单元,
杨氏模量为72000MPa,
泊松比(词条“泊松比”由行业大百科提供)取0.2,有限元网格
密度为100mm。玻璃板块的边界条件与荷载见图3:为了约束转动自由度,使玻璃板块成为静定结构,束缚A点在玻璃平面内的自由度, B点束缚沿玻璃长边方向自由度,以及C点束缚沿玻璃短边方向自由度,D点施加角部翘曲量d。
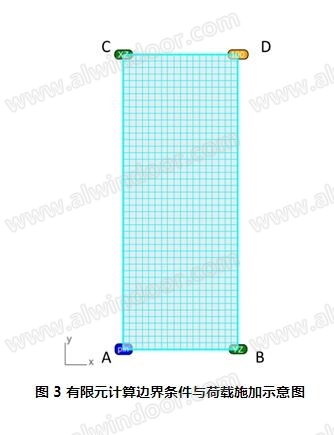
为了考虑玻璃板面的薄膜应力,需激活几何非线性的影响,使用Ansys软件,计算表4中的16个板面,提取每个板面的上下表面上主应力的最大值,进行统计。选取样板编号4#,8#,12#,16#有限元计算板面的变形以及应力分布图如图4。



将以上有限元计算中各个板面的最大应力与公式计算应力进行对比,对比表格见表5,对比曲线见图5:
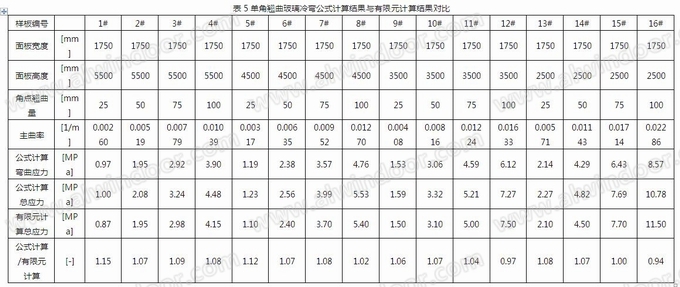
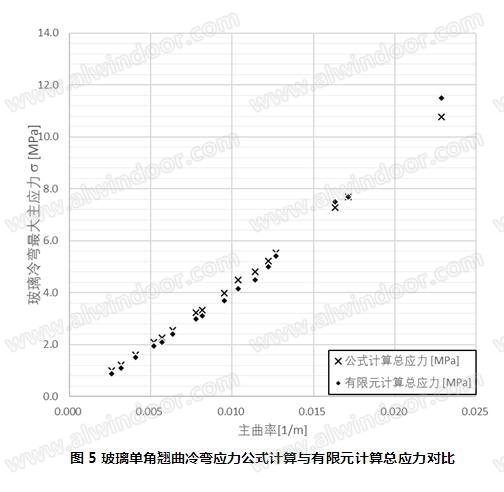
由以上计算结果,可见得出以下结论:
(1) 对于相同尺寸的玻璃板块与相同的角点冷弯量,计入几何大变形与不计几何大变形情况下,玻璃表面的应力分布有所不同。通过计算对比发现,计入薄膜应力后,玻璃中部应力有所下降,玻璃边部应力有所提高,其计入几何大变形后计算出的玻璃表面最大应力出现在玻璃的边缘,并略大于纯弯曲应力。此现象进一步说明单点翘曲的玻璃为大挠度变形,计算需要充分考虑薄膜应力的影响,才能正确的反应玻璃的内力情况。
(2) 由表5以及图5可见,对于相同的玻璃厚度,冷弯应力的大小与板块主曲率呈正比趋势。由此可见,相同冷弯量下冷弯应力的大小与板块的大小相关,即对于相等的冷弯量,玻璃板块越小,对角线长度越短,应力越大。此结论对于工程上具有指导意义,即对于冷弯量的限制应考虑玻璃的板面大小,即应控制冷弯量与板面对角线的比值,而非单纯的控制冷弯量的绝对值。此结论有利于帮助工程师在项目初期判断弯曲玻璃的策略以及对冷弯玻璃或热弯玻璃进行分区。
(3) 由图5可见,公式计算与有限元计算结果相近,误差小于15%。另外,对于角点翘曲量小于1/40玻璃对角线长(即角点翘曲量与对角线长比值小于0.025)的板块,公式计算结果均大于有限元计算结果,即公式计算可以保持比较好的精度且偏保守;对于角点翘曲量大于1/40玻璃对角线长的板块,公式计算结果稍小于有限元计算结果,即公式计算不够保守,即对于10mm厚的玻璃板块,以上公式的适用范围为翘曲量小于1/40对角线长。建议工程中对于特定的玻璃板块厚度,首先根据有限元方法判定此公式的翘曲量限值,以确定公式的适用范围,以便更准确和保守的应用。
2.2 对边起拱冷弯荷载下单片玻璃应力计算简化公式
2.2.1 对边起拱冷弯荷载下单片玻璃弯曲应力
对于对边起拱状的冷弯形式,以弯曲应力为主。根据简支梁的弯矩与曲率的关系,此变形状态下板面弯矩为:

 2.2.2 对边起拱冷弯荷载下单片玻璃应力计算简化公式的有限元验证
2.2.2 对边起拱冷弯荷载下单片玻璃应力计算简化公式的有限元验证
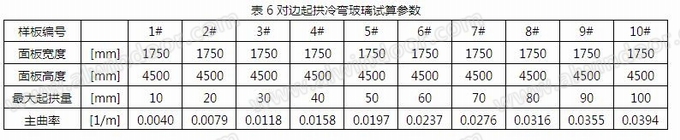
类似于角点翘曲冷弯,同样利用Ansys软件建立有限元模型施加玻璃对边起拱冷弯荷载,与以上玻璃应力公式计算的结果进行对比。对于典型板块的尺寸以及翘曲量见表4。
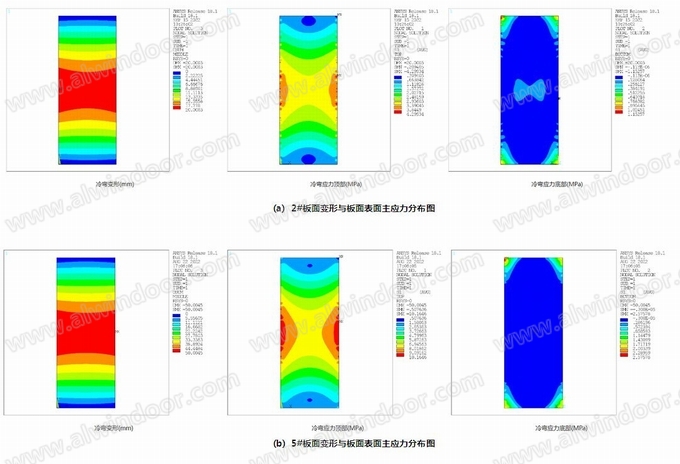
类似于角点翘曲有限元计算,考虑大挠度变形,即几何非线性的影响,使用Ansys软件,计算以上10个板面,提取每个板面的上下表面上主应力的最大值,进行统计。选取样板编号2#,5#,9#有限元计算板面的变形以及应力分布图如图6:

将以上有限元计算中各个板面的最大应力与公式计算应力进行对比,对比表格见表7,对比曲线见图7:
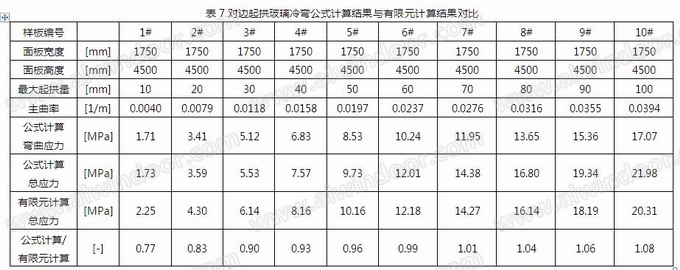
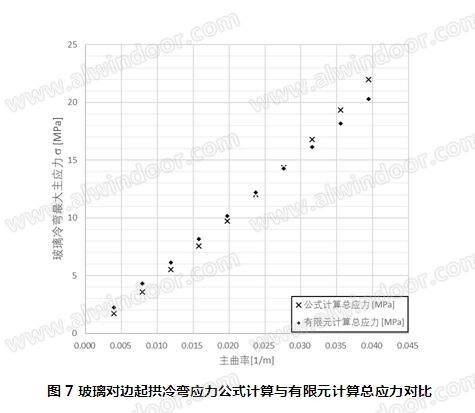
由以上计算结果,可见得出以下结论:
(1) 类似于角点冷弯,对于相同的玻璃板块与相同的冷弯量,计入几何大变形与不计几何大变形的计算对比发现其玻璃表面的应力有所不同,即计入薄膜应力后,玻璃中部应力有所下降,玻璃边部应力有所提高,其最大应力出现在玻璃的边缘,并略大于弯曲应力。此现象进一步说明边部起拱冷弯玻璃亦为大挠度变形,计算需要充分考虑薄膜应力的影响,才能正确的反应玻璃的内力情况。
(2) 由图7可见,对于相同的玻璃厚度,冷弯应力的大小与板面弯曲主曲率呈正比趋势。对于工程实际,可以通过控制起拱量与起拱边边长的关系,作为初步评估允许冷弯量以及区分冷弯玻璃和热弯玻璃的界限的评估标准。
(3) 由图7可见,公式计算与有限元计算结果相近但略有偏差。对于小翘曲量计算,公式计算略小于有限元计算,是因为边部起拱应力最大值对玻璃有限元单元大小以及施加冷弯强制位移的点位距离模拟等较为敏感(见图6a),当冷弯量较小应力较小的情况下,在施加冷弯应力的作用点处会出现一定程度的应力在局部偏大的现象,可认为是数值模拟的偏差;另外,手算公式由于采用简支梁应力与变形公式,即计算时考虑平截面假定成立,然而,由变形图可见,由于冷弯荷载仅施加在玻璃边缘处,在玻璃中部位置玻璃的变形和应力均小于边部,呈现不均匀分布的特点,平截面假设不再成立,此现象也为手算与有限元计算略有差别的原因。由图7可见,此数值模拟以及玻璃跨中与边部不一致的偏差对于拥有较大冷弯量的板块不明显,且对于大冷弯量情况,手算计算结果偏保守。
综上所述,在实际应用中,采用以上公式用于初判对边起拱的冷弯应力计算是可以适用的。如对计算精度有较高要求,仍建议采用有限元方法进行复核。
2.3 单点翘曲与对边起拱冷弯对比
根据上述研究结果,对于相同尺寸和厚度的玻璃板块,分别将相同的冷弯量d施加在玻璃上,即最大冷弯量d位于玻璃的角点处(工况一)和最大冷弯量d位于玻璃长边起拱拱高处(工况二)。运用以上公式,对比以上两种工况下玻璃表面产生的最大主应力值,以及提取计算过程中玻璃弯曲的曲率半径。计算结果汇总见表8.
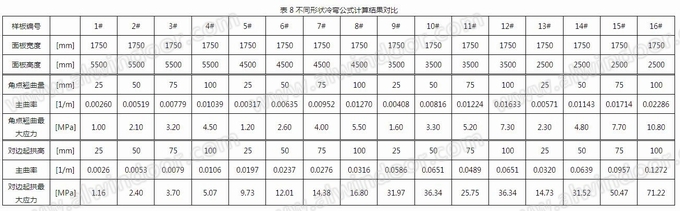
将两种冷弯形式导致玻璃弯曲的曲率半径与玻璃表面最大主应力的关系绘制在同一张图表中,如图7所示。
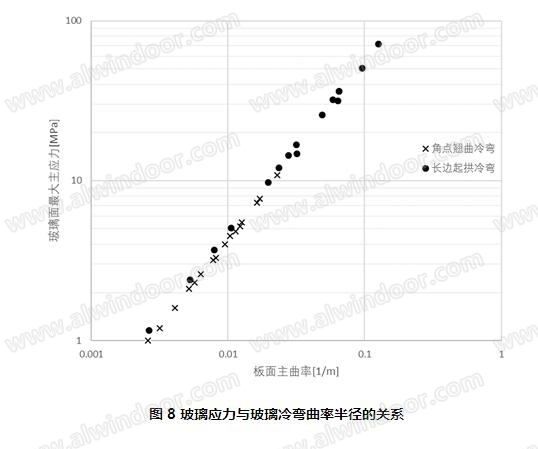
由以上结果可以看出,对于同样尺寸和厚度的玻璃,对于玻璃施加相同的最大冷弯量,此冷弯量施加在单个玻璃角点所产生的玻璃应力远小于将此冷弯量施加于玻璃边长中点使其玻璃起拱产生的应力。这是由于玻璃冷弯产生的应力主要是由于玻璃弯曲导致的,相同的冷弯量如果作用在玻璃单个角点,使得整个玻璃产生的曲率较小从而应力较小,而玻璃对边起拱会导致玻璃产生较大的曲率从而应力较大。通过将两种冷弯变形产生的玻璃弯曲曲率半径与玻璃主应力的关系进行对比(见图8),可以发现,无论是何种形式的冷弯,其冷弯应力与玻璃曲率半径呈相近的相关关系。可以推测,对于任意形状冷弯玻璃,也可以通过量化玻璃冷弯变形前后曲率的最大变化量的方法初步估算该玻璃的冷弯应力,以满足工程初步设计的要求。
工程上的传统做法中,往往不考虑玻璃板块大小和冷弯的具体形态,对比目标曲面与原始曲面的最大差值作为玻璃面最大冷弯量,无论此最大冷弯量出现在角点或是边部,无区别地将此最大冷弯量与容许冷弯量进行对比,作为判定板面是否可以通过冷弯来实现的依据。然而,通过以上结果可知,对于不同的冷弯形态,相同的最大冷弯量可能产生截然不同的内力分布,最大内力可能会有成倍的区别,采用同一容许冷弯量来进行玻璃选型判定的方法并不科学。
根据本文的研究成果,对于符合以上两种常见冷弯形式的玻璃,可配合几何参数提取的方法,通过平板拟合方式,可以方便的提取出每片玻璃板块的单点翘曲值和近似对边起拱值,利用公式(11)与(16),可快速估算出玻璃的冷弯应力。同时,公式的运用相比有限元的方式更加便捷,对于冷弯形态各异的建筑形态,对于玻璃容许应力的判定将不再依赖于制定容许冷弯量这个有局限性的方法,也不必在初步设计阶段为了获得正确的计算结果耗费大量的计算资源进行全楼玻璃有限元计算。运用以上方法,即可方便的对每片玻璃的应力进行初步判定,以指导玻璃类型分区以及指导建筑与幕墙设计。
另外,通过以上公式推导和算例的对比,发现玻璃的冷弯应力与玻璃曲率变化量有直接关系,此结论也给任意形状冷弯计算以及非平板玻璃冷弯计算打下理论基础,作为深化研究计算的开端。
3 结论
为了适应日益复杂的建筑外立面的设计以及满足大批量玻璃冷弯计算的需求,本文从玻璃冷弯变形的原理出发,考虑几何非线性的影响,通过玻璃弯曲形状计算弯曲应力以及通过规范公式等效简化计算薄膜应力的方法,对于常见的冷弯类型(单点翘曲和长边起拱),推导出简单易行的玻璃冷弯应力计算公式,并通过有限元软件非线性计算,验证了简化公式的准确性和保守性,并界定了简化公式的应用范围。
本文中进一步运用以上简化公式,对角点翘曲冷弯与边部起拱冷弯产生的应力进行参数分析,发现在相同最大冷弯量下,以上两种冷弯形式造成的玻璃应力差距大,即玻璃的冷弯应力与玻璃弯曲最大曲率而非最大冷弯量息息相关,故传统方法中不加区分冷弯形式采用单一最大冷弯量来作为玻璃冷弯界限值的方法来对建筑物玻璃类型选择(冷弯玻璃与热弯玻璃选择)并不准确,而需根据实际玻璃冷弯形式和板面尺寸等来区别对待。为了减少根据玻璃实际复杂形态建立大量有限元模型计算带来的巨大计算代价,本文中较高精度的简化公式给工程上快速批量计算异形冷弯带来了可能性。另外,通过参数分析的统计发现,两种截然不同的冷弯形式下,相同厚度的玻璃冷弯应力与弯曲曲率之间的函数关系基本一致,此结论也为任意形状冷弯计算以及曲面玻璃冷弯计算简化公式的推导,奠定了基础。
参考文献
[1]. 《玻璃幕墙工程技术规范》JGJ102-2003,2003,中华人民共和国建设部
[2]. L. Galuppi, S Massimiani, G Royer-Carfagni, Buckling phenomena in double curved cold-bent glass, International Journal of Non-Linear Mechanics, 64(2014) 70-84
作者单位:阿法建筑设计咨询(上海)有限公司
