从非定长优化下料问题的描述及所建立的数学模型可以看出,非定长优化下料问题从本质上可以看作无原材料最大数量限制且原材料规格种类很多的优化下料问题。由于要满足下料方案的可制造性要求,且原材料规格种类很多,不能按一般的多原材优化下料算法处理,本文采用基于下料零件数量整数分解的枚举算法解决非定长优化下料问题。
1.2 定长优化下料阶段
在非定长优化下料阶段,每种切割方式中最多零件种类数和最少原材料定购数量的限制,会导致部分零件未下完,这部分零件的下料,以高原材料利用率为目标,按定长原材优化下料问题处理。其数学模型如下式描述。

定长原材优化下料问题的求解可以采用线性规划方法、动态规划方法等常规方法,也可以采用遗传算法、模拟退火算法等智能算法。本文采用列生成算法求解定长原材优化下料问题[7-8],算法将原线性规划问题分解为主问题和子问题,无需枚举所有可能的排样方式,缓和了由于巨大数量排样方式造成的困难[9]。






在非定长优化下料处理阶段,由于考虑下料方案可制造性的要求,对每种切割方式中套裁的零件种类数有限制,套裁的组合方式会大大降低,降低了求解问题的时间复杂度,采用对零件数量整数分解的枚举算法不会导致运算时间过长。在定长优化下料处理阶段,虽然定长优化下料的背包问题是具有最高计算复杂性的NP完全问题,但在两阶段列生成算法中,经过非定长下料阶段已经处理完大部分的零件,降低了下料问题的规模,使定长优化下料阶段背包问题的求解复杂度降低。
两阶段一维优化下料方法中,在非定长优化下料处理阶段限制了每种切割方式中套裁的零件种类数,套裁的组合方式降低,会减少切割方式的种类数,提高下料方案的总体可制造性;而原材料尺寸根据零件尺寸组合反推,会消除套裁组合方式降低对原材料利用率的影响。在定长优化下料处理阶段,是以最高原材料利用率为目标,可提高下料方案的总体原材料利用率;由于经过非定长下料阶段已经处理完大部分的零件,下料问题规模变得很小,在此阶段没考虑下料方案的可制造性不会对下料方案的总体可制造性带来很大影响。通过两阶段的处理,可以在维持高原材料利用率的同时,大幅度提高下料方案的可制造性。
3 实例与分析
某
门窗(词条“门窗”由行业大百科提供)生产企业拟采用某种切割设备对一批
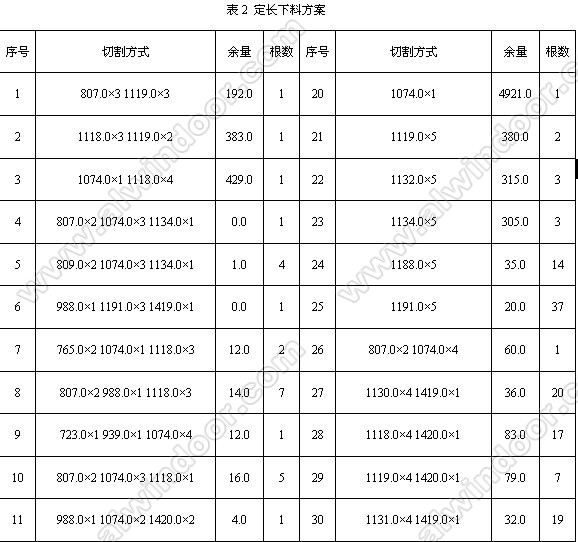
铝合金型材进行下料:表1是待下料零件规格与数量,切割料缝为5 mm。表2是采用国863/CIMS目标产品“建筑
金属(词条“金属”由行业大百科提供)结构计算机辅助设计与生产管理集成系统”中的条材优化下料子系统按定长原材料6000 mm得到的切割方案。表3、4分别是采用本文下料方法编制的优化下料程序非定长处理阶段和定长处理阶段得到的切割方案。其中原材料定购尺寸区间为3000 mm~6000 mm,定购尺寸步长为300 mm,原材料最少定购数量为6支,每种切割方式中零件套裁种类数量限制为1。



 上一页123下一页
上一页123下一页