1.前言
建筑玻璃在风荷载作用下是典型的薄板弯曲问题,薄板在垂直荷载作用下的弯曲同题在弹性力学中有解析解,可准确计算薄板中最大弯曲应力和位置以及最大挠度和位置。但弹性力学解决薄板弯曲问题的基本假设之一是薄板的最大挠度不超过板厚的三分之一,建筑玻璃厚度一般为4m一15mm之间,在弹性力学范围内允许的玻璃挠度变形一般为lmm一5mm,而实际上玻璃在风荷载作用下的挠度变形一般可达几十毫米,甚至上百毫米,已远远超出弹性力学的适用范围,继续采用弹性力学的方法计算出的结果过于保守,原因是其几何非线性必须加以考虑。目前在日本和澳大利亚采用一种半理论、半经验的计算公式,经试验验证,计算结果与实验结果比较符合。日本的公式:

在公式(1)、(2)和(3)中,对于任何长宽比的矩形玻璃,都采用同一面积,这里存在着误差,因为同等面积条件下,不同长宽比的矩形玻璃,其
承载力是不同的。对于
平板玻璃、
半钢化玻璃和
钢化玻璃.仅采用抗
风压调整系数处理也存在着误差,因为这三种玻璃沿玻璃
断面的
内应力分布是不同的,因此其承载力也不同。由于玻璃在风荷载作用下的
力学性能研究试验量巨大,耗时长,因此各国在当时基本上都是采用类似的计算方法,我国的工程行业标准《建筑玻璃应用技术规程》
JGJ113-2003也采了这种方法,基本能满足设计要求。
澳大利亚国家标准AS1288 2006版中采用了新的方法,考虑了矩形玻璃长宽比的影响,将原来计算
玻璃板面积,改为计算不同长宽比条件下的最大跨度。考虑了不同种类玻璃的各自特性,对
平板玻璃、半钢化玻璃和钢化玻璃分别采用不同的计算参数。
中空玻璃由原来两片玻璃同时考虑,改为按荷载分配系数各自独立计算,同时增加了玻璃板挠度限值计算方法,其精确度比1989版的更高、更合理、更全面,本文在此介绍这种新方法。
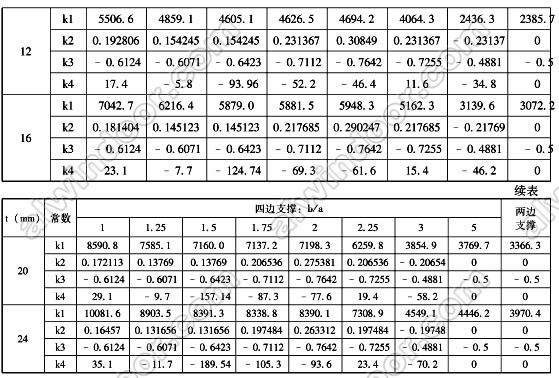
2.玻璃承载力极限状态计算

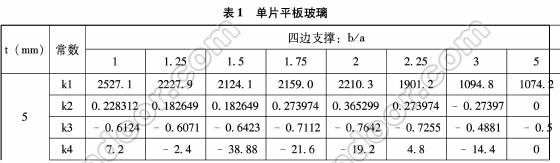

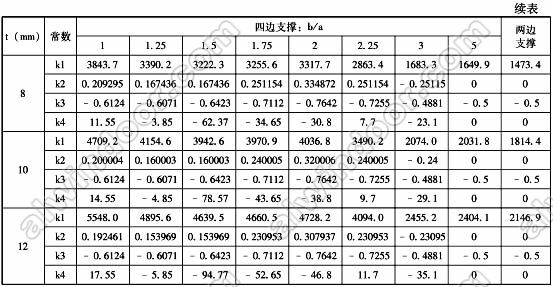


表3 半单片钢化玻璃


 上一页12下一页
上一页12下一页
