摘 要:本文根据试验,当短跨度与全跨跨度比例较小时,按不等双跨
连续梁力学模式设计的
幕墙立柱,其计算结果与试验结果比较存在较大偏差,并对其原因进行分析提出建议.
关键词:不等双跨连续梁;幕墙立柱
一、引言
在目前的幕墙设计中,当主体建筑的楼层跨度较大时,幕墙立柱通常会按不等双跨连续梁的力学模型进行设计。但这种幕墙立柱与
主体结构的连接形式,在当双跨梁短跨跨度与全跨跨度比例较小时,立柱的计算结果与实际状态是否一致呢?通过工程试验,笔者按短跨与全跨比例n≈0.10的情况下,按
挠度分别通过计算结果及试验结果进行比较,得到一个比较直观的概念。
二、理论计算结果与试验结果的比较
(一)不等双跨连续梁短跨与全跨比例n≈0.10
1、试验参数
幕墙立柱跨度L=4.505m,短跨L1=0.45m,长跨L2=4.055m,短跨与全跨比例n≈0.10,幕墙分格宽b=1.237m。选用
铝合金型材,E=0.7 x 10
5N/mm
2;立柱
截面惯性矩I=542.248cm
2。
2、立柱挠度理论计算结果
根据《建筑结构静力计算手册》表3-9以及不等双跨梁的计算方法(此处略)得:跨中最大挠度处与C
支座的距离x=0.5656x4055=2293.51mm;跨中最大挠度系数μ=0.1473 ,分别按幕墙面
荷载,计算幕墙立柱挠度,结果如表1所示。
3、立柱挠度试验结果
根据上海
建筑门窗检测站对此幕墙结构进行
风压变形性能试验,得到结果如表2所示。

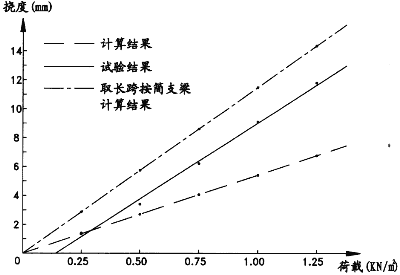
4、立柱挠度结果的比较(见图)
从荷载一挠度图可以看出:(1)理论计算挠度最大点(0.5656 L
2)应接近0.55测点处,但通过测试发现,当风压达到1.0KN/m
2以上,三处测点中0.5处挠度最大。0.45及0.55处的挠度已经小于0.5处,即理论计算挠度最大点(0.5656L
2)处实际挠度也已小于测点0.5处的实测挠度;(2)试验结果大于计算结果,而更接近于取长跨跨度(4.055m)按
简支梁计算所得挠度(计算从略);(3)随着荷载的增大双跨梁的实测挠度与理论计算挠度偏差越大。
 上一页12下一页
上一页12下一页
