本篇文章内容由[中国幕墙网ALwindoor.com]编辑部整理发布:
提要:作为一种人造板材,空心陶板的结构计算比较麻烦。本文通过理论推导公式后,与有限元计算结果进行对比,两种计算结果基本吻合,来验证理论推导公式的可行性。
关键词:空心陶板,计算公式

前言
空心陶板的面板强度计算一直以来比较混乱,绝大多数设计人员都是用空心陶板的总厚度按实心板的计算公式进行计算,包括百度上搜到的关于陶板的强度计算也是如此,存在一定的安全隐患。在《人造板材幕墙工程技术规范》JGJ 336-2016的相关规定中,空心陶板的最大弯曲应力标准值(词条“标准值”由行业大百科提供)宜采用有限元方法(词条“有限元方法”由行业大百科提供)分析计算,也可通过均布静态荷载弯曲试验确定其受弯承载能力,由于采用有限元进行空心陶板建模时比较麻烦,对计算人员要求较高,工程中往往是采用试验的方法来确定其承载能力,即按《天然饰面石材试验方法第8部分 用均匀静态压差检测石材挂装系统结构强度试验方法》GBT 9966.8-2008的相关要求进行均布静态荷载弯曲试验,但是,检测试验相对来说比较麻烦,能否采用理论公式进行计算呢?本文通过理论推导公式和有限元计算结果进行比较,探讨空心陶板的理论计算公式的可行性。
另外,《人造板材(词条“板材”由行业大百科提供)幕墙工程技术规范》中对陶板无挠度计算要求,本文中的挠度公式仅作为理论公式与有限元法之间进行比较验证,也可作为有变形控制要求时的补充计算。
由于空心陶板在长度和宽度两个方向上的截面不一样,截面较复杂,为确保结果准确,特采用了两种有限元软件进行分析,其中,SAP2000(以下简称“SAP”)计算结果明确,可直接查询各点的准确值,但建模相对复杂些,而INVENTOR(以下简称“INV”)建模非常便利,但毕竟不是一种专业计算软件,主要数值可准确查询,但要查询各点的准确值较为困难。通过采用SAP和INV两种有限元,来相互验证计算结果的正确性。
1 理论公式推导
空心陶板的规格较多,宽度一般为300~800mm之间,长度一般不大于1500mm。由于空心陶板通常采用四点支承的固定方式,所以,理论公式也按四点支承进行计算。
1) 基本参数
空心陶板长度为b,宽度为a,厚度为t。另外,空心陶板为小挠度变形,不考虑折减系数。
2) 计算原理
不同于普通的实心陶板,空心陶板长度方向和宽度方向的横截面完全不同,造成横截面惯性矩和抵抗矩也不同,无法采用统一的公式进行计算,所以,考虑采用长度和宽度两个方向分别进行计算。
首先,根据弹性小挠度矩形板计算理论,计算矩形四角支承板两个方向的最大弯矩,并假设两个方向的最大弯矩均布在各自的横截面上;其次,分别计算两个方向的截面惯性矩和抵抗矩,可采用Autocad等软件直接求出,其中,长度方向截面为空心陶板的常见横截面(如图1),惯性矩和抵抗矩分别为Ia和Wa(取较小值),宽度方向为上下两个板厚、中间空心的横截面(如图2),惯性矩和抵抗矩分别为Ib和Wb(取较小值);最后,计算出空心陶板两个方向上的强度以及最大挠度值。

图1 空心陶板长度方向横截面示意图

图2 空心陶板宽度方向横截面示意图
3) 空心陶板两个方向上的弯矩
按弹性小挠度矩形板理论,陶板两个方向上的弯矩系数和跨中最大挠度系数按图3的四角支承板计算简图进行计算,具体数值可从《建筑结构静力计算手册》或相关规范中查表得出,查表时需对。由于最大弯矩系数在面板两个方向自由边中点位置,故两个方向中心点mx和my位置无需计算。
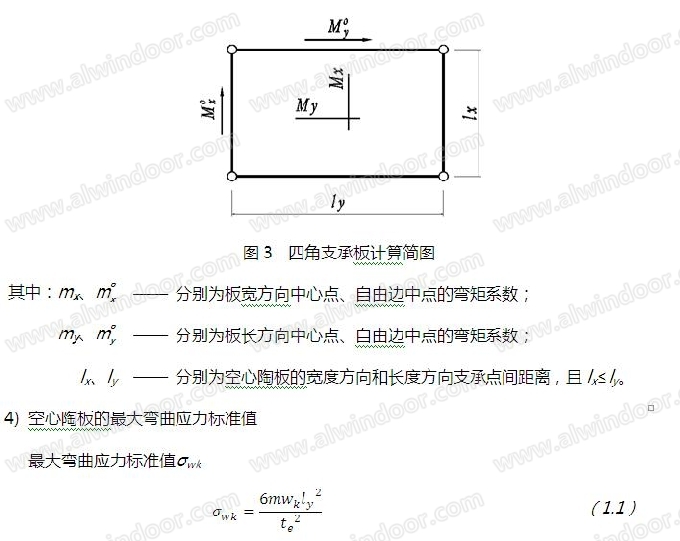

2 理论公式与有限元法对比
考虑到目前陶板的规格尺寸越来越大,同时宽度方向上自由边中点弯矩也较大些,本文采用宽度较大的500mm陶板进行理论公式和有限元法的对比计算,选取陶板宽度500mm,厚度30mm,长度从600~1500mm为分析对象,四角支承仅承受风荷载,风荷载标准值为1.0kN/m2,设计值为1.5kN/m2,不考虑板自重影响。
为方便采用有限元进行建模计算,图4中陶板的截面形状及空心截面的尺寸进行了局部调整,理论公式推导及有限元法的计算均按此截面进行分析。由于空心陶板截面比较复杂,本文采用INV和SAP两个有限元软件进行分析。
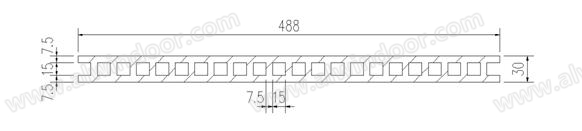
图4 空心陶板宽度方向横截面示意图



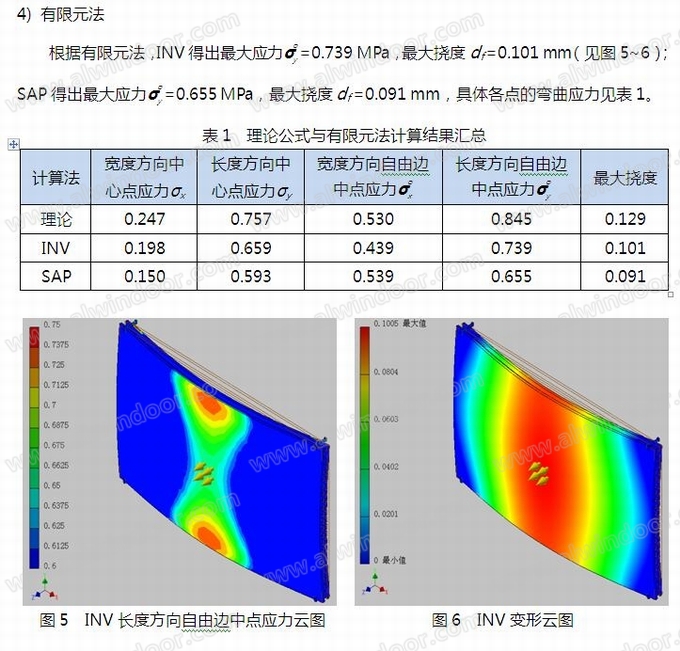
5) 理论公式和有限元法的对比与分析
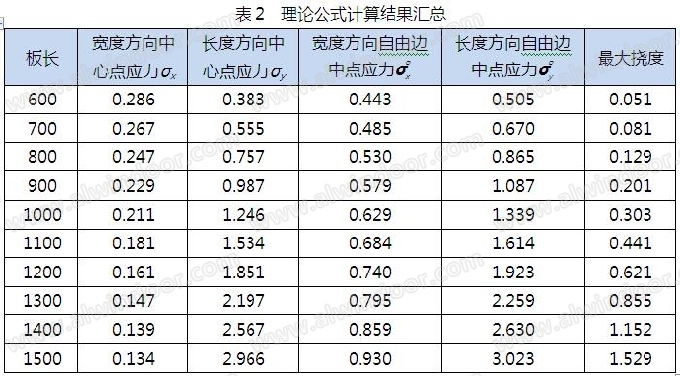
采用理论公式和有限元法分别对从600~1500mm不同板长的空心陶板进行计算,理论公式的结果见表2,有限元INV的结果见表3,有限元SAP的结果见表4。
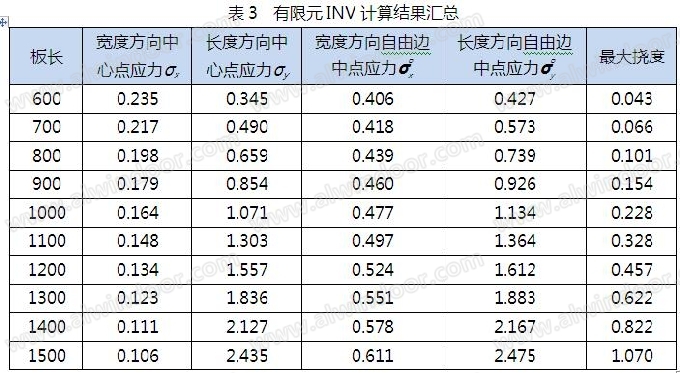
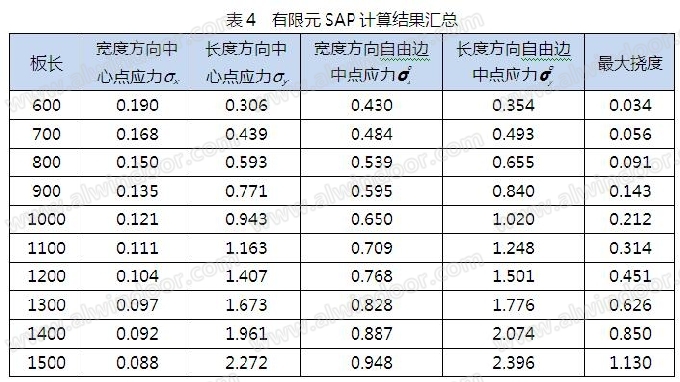
现将空心陶板长度方向自由边中点和中心点的弯曲应力进行对比,具体见图7~8。从图中可以看出,理论公式完全包络了有限元,两个有限元计算结果基本吻合。
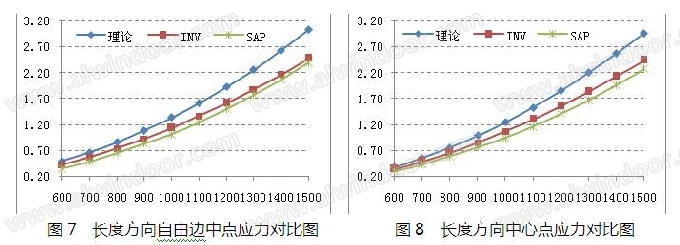
空心陶板宽度方向自由边中点和中心点的弯曲应力对比见图9~10。从图中可以看出,自由边中点的弯曲应力中,理论公式没有完全包络有限元,与SAP的计算结果基本接近,并且SAP与INV有一定的差异,但中心点的弯曲应力则完全包络。
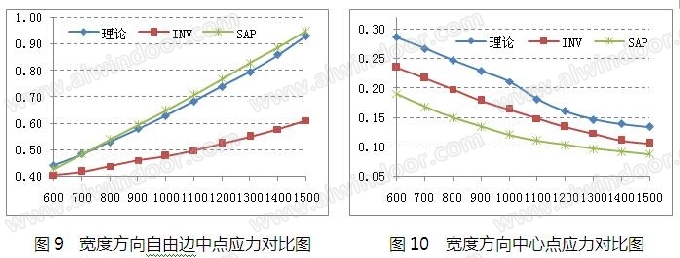
最后,对陶板的最大挠度进行对比,具体见图11。从图中可以看出,理论计算完全包络了两个有限元法,且挠度值远小于板厚,符合小挠度变形理论。
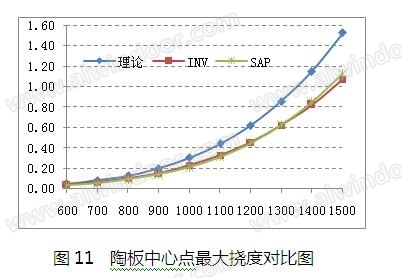
从汇总的计算结果对比来看,理论公式在强度和挠度计算上基本上都包络了两种有限元的计算结果,空心陶板的最大应力在两个方向自由边中点,而两个方向中心点位置可不计算。
3 结论
根据理论公式和有限元法的计算比较,可以得出以下结论:
1) 虽然本文只分析了500mm宽、30mm厚的空心陶板,但计算了长度从600~1500mm 的受力情况,具有很好的代表性,无需再分析其它规格的面板;
2) 空心陶板理论公式和有限元法在个别位置虽然有一定偏差,但最大强度和挠度计算结果均能包络有限元法,且有一定的安全富余,所以,空心陶板采用本文的理论公式进行强度和挠度进行计算可行;
3) 从挠度计算结果可以看出,空心陶板最大挠度远小于板厚,且数值很小,均为小挠度变形,不考虑折减系数。根据相关规范要求,除特别要求外,无需进行挠度计算;
4) 空心陶板的最大应力在长边和短边自由边中心mo x和mo y位置,如果空心陶板的长度小于或与宽度尺寸接近时,应分别计算长边和短边自由边中心的强度,从中选取相对位置的最大应力;如长度大于宽度时,只需计算长度(词条“计算长度”由行业大百科提供)方向自由边中心mo y位置的最大应力;
5) 如陶板采用非四点支承的其它固定方式,强度和挠度计算公式应按相关规范进行相应调整。
[参考文献]
[1] 《建筑结构静力计算手册》编写组主编. 建筑结构静力计算手册. 北京:中国建筑工业出版社,1999.
[2] 《人造板材幕墙工程技术规范》JGJ 336-2016. 北京:中国建筑工业出版社,2016.
作者单位:深圳市建筑门窗幕墙学会

