1.概述
玻璃幕墙具有高雅美观、经久耐用和装配高效等优点而被广泛应用于现代土木工程建筑之中。尤其是在高层和超高层建筑中,玻璃幕墙作为建筑外围防护的一种重要形式具有显著的优势。为了适应不同的建筑风格和功能要求,玻璃幕墙中玻璃的种类各式各样。从组成结构上分主要有单片玻璃、中空玻璃和夹层玻璃等;从制作工艺上分主要有单片热弯玻璃(词条“热弯玻璃”由行业大百科提供)和球形夹层热弯玻璃等。
玻璃是一种抗压强度较高的脆性材料,产生脆性破坏时的变形(词条“变形”由行业大百科提供)相对于龙骨材料要小许多。因而对玻璃幕墙的挠度的控制尤为重要,这也是玻璃幕墙在抗风设计中的一项重要指标。不同形式的玻璃幕墙在承受风压时表现出来的性能是不同的,其压力差与挠度之间的规律也有所差异。已有学者对支点式单层玻璃幕墙、夹板式夹层玻璃幕墙、铝塑复合板幕墙的抗风性能进行相关的分析和探讨,然而对于中空玻璃幕墙的抗风性能的研究却很少。为了进一步明确中空玻璃幕墙的抗风性能,即压力差与挠度之间的变化规律,本文利用幕墙动风压测试设备对中空式玻璃幕墙的抗风压性能进行了试验研究。并将试验结果与理论计算结果进行了对比分析,以期为工程建设提供参考。
2.玻璃幕墙抗风压试验
2.1试验概况
中空玻璃幕墙抗风压性能试验试件尺寸为宽2175mm×高3600mm。嵌板材(词条“板材”由行业大百科提供)料为玻璃面板,Low-E 6+12+6mm中空钢化玻璃,室内的一片为镀膜低辐射钢化玻璃。玻璃最大尺寸为1000mm×1700mm。采用湿法镶嵌方法,采用硅酮密封胶(词条“硅酮密封胶”由行业大百科提供)密封。试验时的环境温度为26℃,气压为101.5kPa。支承体系采用铝合金龙骨架,主龙骨尺寸为120mm×65mm,次龙骨尺寸为65mm×65mm。
2.2测点布置
在抗风压性能试验中,分别在中空玻璃面板中线和玻璃幕墙试件中线处布置了2组测点。在相应的测点处安装数码位移计,位移计安装在中空玻璃面板和玻璃幕墙的外侧。用来测定在不同的压力差作用下,玻璃面板和玻璃幕墙试件的挠度的变化规律。玻璃面板和幕墙的面法线挠度测点布置情况如图1所示。
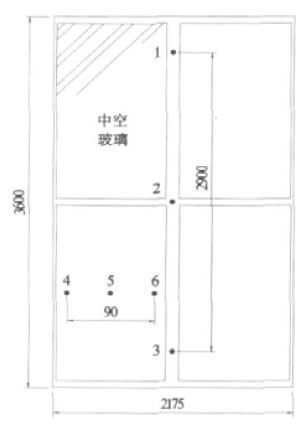
图1 试验测点布置示意图(单位:mm)
2.3试验及结果
将玻璃幕墙固定于试件安装系统上并将玻璃幕墙与压力箱开口部位密封,供风设备施加正负双向压力。在正负压检测前分别施加3个压力脉冲。压力差绝对值为500Pa,加压速度为100Pa/s,持续时间为3s,待压力差回零后开始进行试验。试验过程依据《建筑幕墙气密、水密、抗风压性能检测方法(GB/T15227-2007)》和《建筑幕墙(GB/T21086-2007)》的规定进行操作。试验中加载方案如图2所示(图中符号▼表示将试件的可开启部分开关5次,图中的最大压力差满足Pmax>P3)。

图2 加载方案示意图
试件的面法线挠度是衡量构件抗风压性能的主要指标。本试验中,受力试件的面法线挠度按照下式计算:

式中,f为面法线挠度值,(mm);a0、b0和c0分别为各测点在预备加压后的稳定位移值,(mm);a、b和c分别为某级试验压力作用过程中各测点的面法线位移,(mm)。
根据试验得出的各测点的位移计算铝合金玻璃幕墙构件和中空玻璃中心点处的挠度。幕墙试验构件中心点的挠度以及中空玻璃中心点的挠度随压力差的变化规律如图3所示。从图3可以看出,铝合金(词条“合金”由行业大百科提供)玻璃幕墙构件中心点处的挠度随着压力差的增大呈近似线性增加。正压力差为1250Pa时,构件中心点处的最大挠度为6.01mm;相应的负压力差作用下的构件最大挠度为-6.34mm,二者相差5%。构件中的中空玻璃中心点处挠度也随着压力差的增大呈近似线性增加的变化规律。最大正压力差作用下,中空玻璃中心点处的挠度为3.81mm,相应的负压力差作用下的最大挠度为-3.79mm,二者相差不到1%。

图3 试件和中空玻璃中心点挠度随压力差的变化规律
3.理论分析
3.1挠度计算
针对中空玻璃幕墙的特点,由于其变形较小,一般小于玻璃的厚度。因而,可以采用《玻璃幕墙工程技术规范(JGJ102-2003)》中的小挠度计算理论来计算其跨中挠度。但是在确定其厚度时,应采用等效厚度。中空玻璃构件的刚度可以按照下式确定:
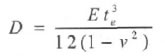
式中,D为中空玻璃构件的刚度,E为玻璃的弹性模量(词条“弹性模量”由行业大百科提供),(N/mm2);te为中空玻璃的等效厚度,(mm);v为泊松比。中空玻璃的等效厚度t由下式计算:

式中,k为等效厚度系数,取k=0.95;t1和t2分别为各单片玻璃的厚度,(mm)。对于玻璃的跨中挠度,按照考虑几何非线性(词条“非线性”由行业大百科提供)的有限元方法计算,风荷载作用下最大挠度由下式计算:

式中,wk为垂直于玻璃幕墙平面的风荷载标准值(词条“标准值”由行业大百科提供),(N/mm);a为玻璃短边变长,(mm);μ为挠度系数,可由玻璃短边与长边边长比按规范《玻璃幕墙工程技术规范(JGJ102-2003)》确定,η为折减系数,可由参数θ按照规范确定,且:

3.2试验与理论结果对比分析
理论计算中,取玻璃的弹性模量为6.5×104N/mm2,泊松比取0.25。各层玻璃的厚度为6mm,玻璃短边尺寸为1000mm,长边为1700mm。各级压力差荷载作用下相应的参数和折减系数的计算结果见表1。
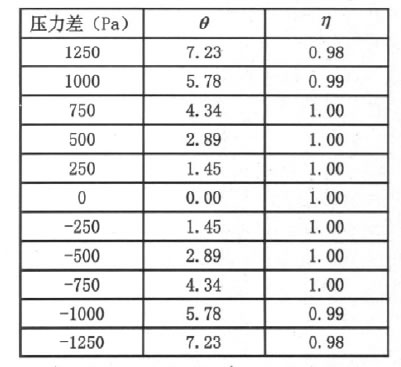
表1 各级压力差下的参数和折减系数
中空玻璃中心点处的挠度的理论解和试验结果如图4所示。由图4可知,理论结果和试验结果具有相同的变化规律,其挠度均随着压力差的增大而近似呈线性增加。当压力差为1250Pa时,理论方法计算玻璃中心点处的最大挠度为5.05mm,而相应的压力差荷载作用下,试验测得的中心点处最大挠度为3.81mm。理论结果比相应条件下的试验结果大25%。由此可知,现行的理论方法的计算结果偏于保守,利用该理论方法进行中空玻璃幕墙的设计是偏于安全的。
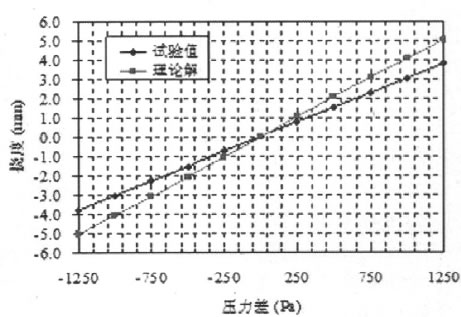
图4 理论与试验结果对比

