1 引言
由于爆炸事件引起的日益严重的后果,如何提高工程结构的综合防护能力,是工程结构必须解决的问题。爆炸产生的脉冲
荷载具有高度的
非线性,并且一般只有几毫秒到十几毫秒的瞬间完成,因此结构的爆炸动力响应十分复杂[1] 。目前,
玻璃幕墙作为建筑的外
围护结构广泛的应用于高层及
超高层建筑中,此类建筑内部人群比较密集,当玻璃幕墙遭受室外突发性爆炸(包括汽车炸弹、人体炸弹等)冲击波作用而发生剧烈破坏,会导致很大的人员伤亡和经济财产损失,其安全性应着重考虑。
动力学研究主要从三个方面进行:理论分析、数值计算和试验研究,其中试验研究占有重要的地位,可以用来证实理论分析和数值计算的结果,同时由于材料动力学涉及的冲击爆炸都是在瞬间完成,以及结构形式的复杂多样和所用材料的多样化使理论研究很难适应工程的需求,因此详细观察这些现象也必须依赖于试验研究[2] ,并基于试验结果建立准确的数值模拟模型,进而为后续的理论分析及数值模拟的准确性奠定基础。本文运用 ANSYS 软件对试验模型进行了数值模拟,并与四边简支单层、
夹胶玻璃面板爆炸作用试验进行了对比,进而得出了较为准确的力学模型。
2 ANSYS 简介
ANSYS 是世界上著名的动力分析有限元程序,可以精确可靠的处理各种高度非线性问题,如碰撞分析、爆炸分析、
冲压成型分析、常规武器设计、跌落分析、热分析及流固耦合分析等。自 20 世纪 90 年代引入国内以来,在汽车、国防军工、电子、制造和建筑行业得到越来越广泛的应用。其也是是功能齐全的几何非线性(大位移、大转动和大应变)、材料非线性(140 多种材料动态模型)和接触非线性(50 多种接触模式)程序,以 Lagrange 算法为主,兼有 ALE 和Euler 算法;以显式求解为主,兼有隐式求解功能;以结构分析为主,兼有热分析、流体-结构耦合功能;以非线性动力分析为主,兼有静力分析功能,是军用和民用相结合的通用结构分析非线性有限元程序[3]。
爆炸动力学过程非常复杂,很难进行精确的解析分析,数值分析与模型试验是目前最常用的两种方法。数值分析的
精度依赖于描述物质的模型(如材料本构关系,炸药状态方程等)、边界条件、荷载条件等。目前情况下,描述爆炸作用下的物质模型还不很完善,数值分析的精度一般不高于近似方程的精度,但是数值模拟可以提供整个过程的现象描述,并且通过拟合参数的方法使得计算结果与试验结果相吻合[4] 。
本文运用显式动力学软件ANSYS研究
玻璃面板在爆炸冲击波作用下的动态响应情况并通过试验结果验证模型的正确性。
3 有限元模型
玻璃面板抗爆数值模拟的准确性离不开合理的材料本构方程、准确的结构模型以及合理的荷载分布形式。根据试验[5]试件(玻璃尺寸为 1000mm×1000mm,厚度分别为 8mm 的单层
钢化玻璃及 6mm+1.14mm+6mm 夹胶钢化玻璃)进行建模。
数值模拟分析中,为了减小计算时间及文件大小,取面板的 1/4 模型进行数值计算。仅针对夹胶玻璃(单层玻璃应用到工程实践中意义不大)分析,其中对称面按对称轴约束,边界采用简支约束。
测点布置如图 1 所示。

图中: d 表示位移测点,测点间距为 200mm;ε表示
应力σ所对应的应变测点,如上图标示。
3.1 单元选择及结构模型
在ANSYS 的单元库中可以选择Shell163 薄壳单元和Solid164 体单元模拟玻璃面板及
PVB 夹胶。Shell163 薄壳单元是可以抵抗面内及法线应力的 4
节点单元,每个节点具有X, Y, Z 方向的平移、速度、加速度及转动共 12 个自由度。Solid164 为 8 节点的体单元,每个节点具有 X, Y, Z 方向的平移、速度、加速度共 9 个自由度。如图2,图 3 所示。
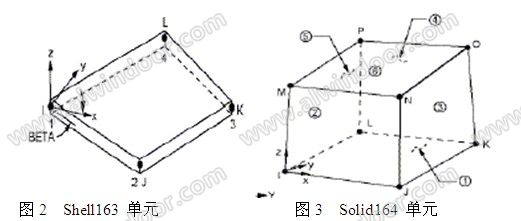
对于单片玻璃,为准确描述出不同层玻璃单元失效过程,采用 Solid164 单元进行模拟。对夹胶玻璃,玻璃与 PVB 界面依靠高压下
加热粘连,其蠕变特性取决于温度及时间,因此在动力荷载作用下,PVB
粘结力相对较高,可以假定玻璃与
夹层的全粘结,胶片的
剥离不予考虑[6] [7] ,故采用玻璃与夹胶共用节点进行有限元分析。
数值模拟夹胶玻璃有主要有三类模型:分布式模型(smeared model)、分层材料模型(layered material model)以及 3D 实体模型(3D model)。3D 实体模型可以更细致的描述夹胶材料的本构关系,基于此模型,Wei J.选用粘
弹性材料模型考虑PVB应变率的影响,但与 shell 单元相比,solid单元计算更加耗时。
综合已有结构模型,为了获得更好的网格质量,得到较高的精度以反映夹胶玻璃层间作用关系,获得不同层玻璃失效过程,本文采用 3Dsolid 模型进行数值分析。
3.2 材料模型
爆炸作用是在极短的时间内(一般为几个到几十个毫秒时间之内)的物理或化学的能量释放过程。具有传播速度快、峰值大、作用时间短等特点。在爆炸空气冲击波荷载作用下,
结构材料受到毫秒级的快速加载,其应变速率可达到102~103/s,而常规静载材料的应变速率为 10-5/s 左右,材料动力快速加载试验表明,随应变速率的提高,材料内部发生了一系列物理化学变化,其力学特性主要表现在应力应变关系更为复杂,一些特征参数,例如
强度、延性、
弹性模量、阻尼比等均有不同程度的变化。大量试验结果表明,在高速加载条件下,材料的
屈服强度明显提高。
玻璃作为
脆性材料,不像
金属等材料可以
弯曲变形,当受到外力作用是,尤其受到的外力超过玻璃本身的
许用应力时,玻璃会发生破碎。其
抗拉强度取决于表面的
裂纹缺陷(不一定肉眼可见),因此尽管玻璃的理论抗拉强度(基于分子力)极其高可达 32GPa,但这只有在玻璃毫无瑕疵时才具备,通常玻璃是有瑕疵的,玻璃表面尤其易被划伤、擦伤或受大气侵蚀,因此在实际结构应用中一旦超过临界应力,玻璃就会脆裂,其抗拉强度比理论低很多。图 4 给出了不同裂纹深度下抗拉强度概述图[8] 9] 。

由上图可以看出:玻璃的抗拉强度不是一个常数。其取决于很多因素,尤其是玻璃表面的条件,玻璃单元的尺寸、厚度,加载历史(强度和持续时间),残余应力和环境条件等。当荷载越大、持续时间越长、初始表面裂纹越深,玻璃的有效抗拉强度越小。
我国《玻璃幕墙工程技术规范》(
JGJ102-2003)中规定:短期荷载作用下,厚度为 5~12mm 的钢化玻璃屈服强度为 84MPa[10] 。在爆炸冲击荷载下,其破坏应力相应于静力荷载下均有所提高。在ANSYS 材料库中[11] ,可采用特定的材料模型模拟玻璃、
陶瓷等脆性材料在冲击荷载作用下的响应。由于在高速冲击荷载作用下,材料模型经历大应变,大应变速率以及高压力过程,因此其状态方程关于应变、应变率及压力范围的参数需要试验来确定,对于钢化玻璃,国内外还没有相应试验数据支持,故本文采用带失效准则的材料模型模拟玻璃破坏[8]。
试验表明,PVB 夹胶的力学性能受加载时间影响很大。在较长的荷载持续时间、小应变速率作用下,PVB 胶片具有粘弹性性质;在较短的荷载持续时间、较高应变速率作用下,材料表现为弹
塑性特性,与其它
塑性材料类似,PVB 在大应变(约 300%)表现出破坏。同时,在高应变率情况下,PVB 胶片的弹性
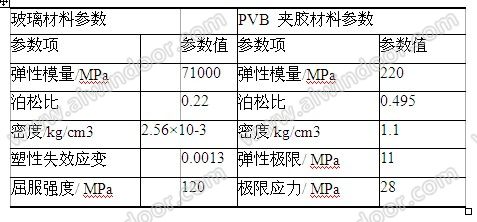
模量也成倍增长[7] 。因此在爆炸冲击荷载作用下,取 PVB 胶片为弹塑性材料模型。玻璃及 PVB 夹胶材料参数如表1所示:
表1 钢化玻璃及 PVB 夹胶材料参数表
4 网格划分
网格划分是建立有限元模型的一个重要环节,所划分的网格形式将直接影响计算精度和计算规模。本文需要模拟玻璃面板在爆炸冲击荷载作用下的破坏,并研究玻璃的
裂缝产生等破坏过程。在多数通用有限元软件中,裂纹的生成与扩展的模拟主要有两种方法:一种是通过单元失效在结构中产生裂纹;另一种是通过定义节点约束失效形成裂纹。在材料模型定义中,将玻璃材料定义了失效准则,因此可以通过第一种方法模拟玻璃的裂纹,但这种方法为降低结果误差,需要将模型划分较细的网格,否则由于大量单元的失效将产生较大的误差。为达到计算精度与计算效率的优化统一,本文采用 1/4 玻璃模型进行计算,在长度方向 100等分且单片玻璃厚度方向划分 3 个单元以上,网格划分如图 5 所示。

5 荷载简化
爆炸冲击波的压力参数和持续时间是决定结构响应的重要参数。对于爆炸动力荷载的模拟,ANSYS 中提供了两种方法,一种为将爆炸荷载简化为力的时程曲线施加到结构面单元上;另一种方法是利用状态方程模拟爆炸过程中压力与体积的关系,模拟炸药与被炸结构之间的关系。本章根据试验[5]实测的爆炸冲击后压力随时间的变化情况(如图6),简化为三角形压力时程曲线施加到玻璃面板上(如图 7)。
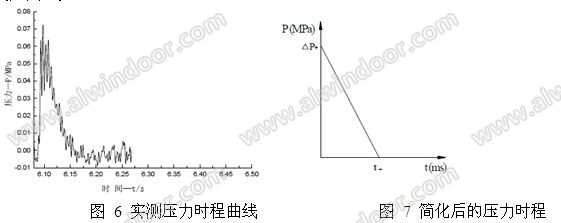
曲线
由上图可看出在爆炸后数毫秒内,试验段内压力由零迅速上升到预定的峰值压力,而后逐步下降到零。因此可将试验实测压力时程曲线测导爆索爆炸时的超压时程曲线简化为三角形荷载。
6 夹胶玻璃数值结果与试验结果对比分析
6.1 破坏形式
根据试验[5]实际施加的荷载(峰压值为 0.07MPa,持续时间为 50ms)进行有限元分析。如图8 所示,夹胶玻璃在试验所施加的荷载下,玻璃面板非受力面碎裂,破损裂纹由中心向外延伸均匀分布,在数值模拟中,在冲击荷载作用下,玻璃背面(非受荷面)跨中首先产生裂纹,随荷载的持续增加,裂纹会迅速
开裂,但玻璃面板仍整体保持完整,PVB 胶片没有破坏,没有产生碎片飞溅,与试验结果相吻合。

6.2 应力时程分析及试验验证
图 9为不同时间段的玻璃面板背面(非受荷面)的应力云图。从图中可以看出,随着荷载持续时间的增加,面板的应力不断增大,直至达到玻璃的屈服应力,玻璃碎裂,随后玻璃面板应力逐渐减小,这与试验实测结果一致,对应测点的应力时程曲线如图 10 所示。
在大约6.65ms,玻璃背面(非受力面)跨中首先产生裂纹,与试验结果相吻合。随着荷载作用时间的增加,面板裂纹不断扩展,玻璃最终完全碎裂。
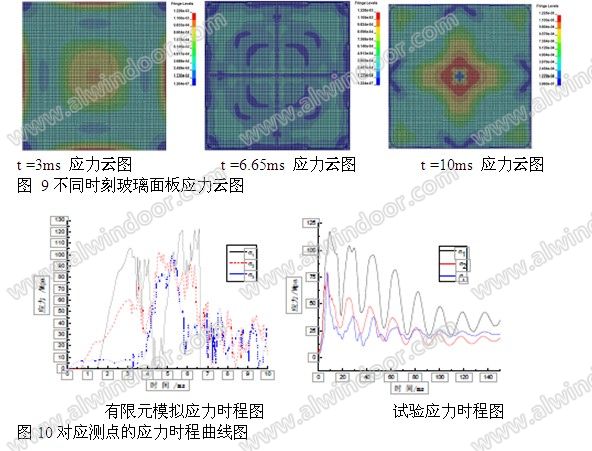
由上图可以看出,数值模拟中,测点应力 σ1(跨中),σ2,σ3 所对应的最大应力分别为 122.6MPa,102.4MPa,99.3MPa,且随着离跨中距离的增加,应力逐渐减小,有限元模拟与试验结果基本吻合。根据《玻璃幕墙工程技术规范》(
JGJ102-2003)中规定:短期荷载作用下,厚度为 5~12mm 的钢化玻璃屈服强度为 84MPa。在爆炸冲击荷载下,其破坏应力相应于静力荷载下均有所提高。与试验结果(σ1=117.3MPa, σ2=80.1MPa,σ3=78.4MPa)相对误差均在 25%以内,误差在允许误差范围内。
6.3 位移时程分析及试验验证
图 11 为有限元分析玻璃面板位移图。从图中可以看出,面板跨中位移最大,且随距离跨中距离的增加位移逐渐减小,与试验结果一致。对应测点的位移时程曲线如图12 所示。
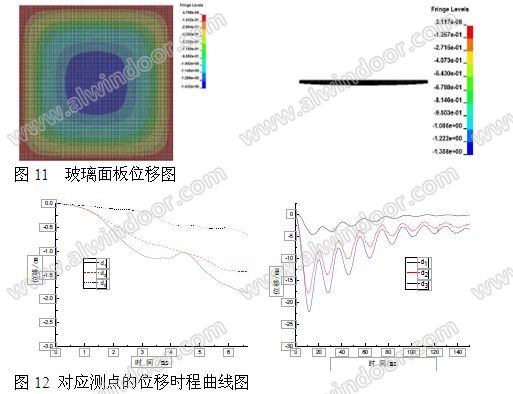
有限元分析中,玻璃面板跨中应力达到最大时(6.65ms),跨中位移达到最大值。有限元模拟结果表明,d1(跨中),d2,d3 位移随时间变化规律一致,位移最大值分别为 18.7mm, 14.2mm, 6.1mm;《玻璃幕墙工程技术规范》(
JGJ102-2003)中规定:在
风荷载等短期荷载作用下,四边简支玻璃面板的
挠度限值宜按短边边长的 1/60 采用,因此由试验[5]结果可以看出:在爆炸冲击荷载下,破坏时其跨中挠度相应于静力荷载下均有所提高。与实测结果(d1=21.5mm, d2=16.9mm,d2=4.7mm)相比,最大位移相差 25%,误差在允许误差范围内。
7 结论
通过对玻璃幕墙在爆炸冲击荷载作用下的动力响应试验和数值分析,可以得出如下结论:
夹胶玻璃能抵抗一定的爆炸冲击波,且破坏后碎片会牢固黏在 PVB 夹层里,不会对人员产生二次伤害,因此可以作为抗爆结构中的
安全玻璃使用。
将试验中测得爆炸冲击波的压力时程按三角形冲击波荷载进行简化,计算结果满足精度要求,表明荷载的简化方法是可行的,可供工程设计参考;
在试验的基础上研究了夹胶玻璃幕墙的动力响应,通过数值模拟的方法得到了与试验结果相一致的结果,证明了数值模拟方法的有效性,为解决工程实际问题提供了参考。
试验结果和数值模拟结果均表明:在爆炸冲击荷载作用下,玻璃面板破坏时屈服应力和位移均大于静力荷载作用下的值。其碎裂时从内层玻璃(非受荷面)开始碎裂,由中心逐渐向外扩展。为玻璃幕墙在爆炸冲击荷载作用下的破坏形式研究提供了参考。
注:本文所用有限元软件,仅针对本文研究用,不作任何其他用途。
参考文献
[1] 史春芳,工程结构抗爆技术的研究现状[J]. 西安建筑科技大学学报,2007,39(5):616-620
[2] 宁建国,王成,马天宝. 爆炸与冲击动力学. 北京:国防工业出版社,2010
[3] 时党勇,李裕春,张胜民. 基于ANSYS/LS-DYNA8.1进行显示动力分析[M ].北京:清华大学出版社,2004
[4] 白金泽.LS-DYNA3D 理论基础与实例分析.北京: 科学出版社,2005: 125 -133.
[5]
陈峻 陶志雄 四边简支玻璃模爆法试验:2012年全国
铝门窗幕墙行业年会论文集
[6] Timmel M., Kolling S., Osterrieder P., Du Bois P., A Finite Element Model for Impact Simulation with Laminated Glass, International Journal of Impact Engineering Vol. 34, 2007, pp. 1465–1478.
[7] Martin Larcher, Norbert Gebbeken, MartienTeich, George Solomos. Simulation of Laminated Glass Loaded by Air Blast Waves. Applied Mechanics and Materials.Vol. 82(2011):69-74.
[8]Matthias Haldimann, Andreas Luible, Mauro Overend. Structural Use of Glass[M]. Switzerland: IABSE-AIPC-IVBH, 2008.
[9] 彼得•赖斯,休•达顿. 索
结构玻璃幕墙[M]. 大连:大连理工大学出版社,2006,2.
[10] JGJ 102-2003.玻璃幕墙工程技术规范.2003.
[11] www.Cadfamily.com. LS-DYNA Keyword User’s Manual[M]. California: LivermoreSoftware Technology Corporation, 2006.
